(本小题满分16分) 对于项数为 的有穷数列
的有穷数列 ,记
,记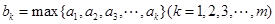 ,即
,即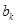 为
为 中的最大值,则称
中的最大值,则称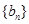 是
是 的“控制数列”,
的“控制数列”,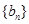 各项中不同数值的个数称为
各项中不同数值的个数称为 的“控制阶数”.
的“控制阶数”.
(Ⅰ)若各项均为正整数的数列 的控制数列
的控制数列 为
为 ,写出所有的
,写出所有的 ;
;
(Ⅱ)若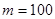 ,
, ,其中
,其中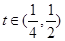 ,
,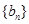 是
是 的控制数列,试用
的控制数列,试用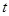 表示
表示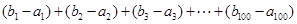 的值;
的值;
(Ⅲ)在 的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
推荐套卷
(本小题满分16分) 对于项数为 的有穷数列
的有穷数列 ,记
,记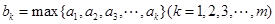 ,即
,即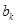 为
为 中的最大值,则称
中的最大值,则称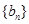 是
是 的“控制数列”,
的“控制数列”,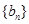 各项中不同数值的个数称为
各项中不同数值的个数称为 的“控制阶数”.
的“控制阶数”.
(Ⅰ)若各项均为正整数的数列 的控制数列
的控制数列 为
为 ,写出所有的
,写出所有的 ;
;
(Ⅱ)若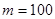 ,
, ,其中
,其中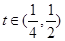 ,
,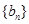 是
是 的控制数列,试用
的控制数列,试用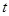 表示
表示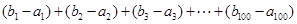 的值;
的值;
(Ⅲ)在 的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.
的所有全排列中,将每种排列视为一个数列,对于其中控制阶数为2的所有数列,求它们的首项之和.