已知f（x）是定义在（0，+∞）上的单调函数，f′（x）是f（x）的导函数，若对∀x∈（0，+∞），都有f[f（x）﹣2x]=3，则方程f′（x）﹣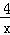
=0的解所在的区间是（ ）
A．（0， ） |
B．（，1） |
C．（1，2） | D．（2，3） |
推荐套卷
已知f（x）是定义在（0，+∞）上的单调函数，f′（x）是f（x）的导函数，若对∀x∈（0，+∞），都有f[f（x）﹣2x]=3，则方程f′（x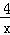）﹣=0的解所在的区间是（ ）
| A．（0，） |
B．（，1） |
C．（1，2） | D．（2，3） |
粤公网安备 44130202000953号