在实数集R中定义一种运算“⊕”，具有性质：
①对∀a，b∈R，a⊕b=b⊕a；
②对∀a∈R，a⊕0=a；
③对∀a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c；
那么函数f（x）=x⊕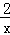
（x≥1）的最小值为（ ）
| A．5 | B．4 | C．2+2 |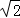
D．2 |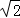
相关试题
，则f[f（1）]＝（）
∈A
A
推荐套卷
在实数集R中定义一种运算“⊕”，具有性质：
①对∀a，b∈R，a⊕b=b⊕a；
②对∀a∈R，a⊕0=a；
③对∀a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c；
那么函数f（x）=x⊕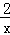（x≥1）的最小值为（ ）
| A．5 | B．4 | C．2+2 |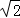
D．2 |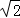
粤公网安备 44130202000953号