甲、乙两名同学参加一项射击比赛游戏，其中任何一人每射击一次击中目标得2分，未击中目标得0分．若甲、乙两人射击的命中率分别为
和P，且甲、乙两人各射击一次得分之和为2的概率为
．假设甲、乙两人射击互不影响，则P值为（ ）
| A． |
B． |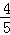
C． |
D． |
相关试题
，则
等于
，
，
，则
中，点
为
中点，
，则
等于
推荐套卷
甲、乙两名同学参加一项射击比赛游戏，其中任何一人每射击一次击中目标得2分，未击中目标得0分．若甲、乙两人射击的命中率分别为和P，且甲、乙两人各射击一次得分之和为2的概率为．假设甲、乙两人射击互不影响，则P值为（ ）
| A． |
B． |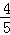
C． |
D． |
粤公网安备 44130202000953号