将一张边长为6 cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折叠并拼成一个有底的正四棱锥（底面是正方形，顶点在底面的射影为正方形的中心）模型，如图2放置，若正四棱锥的正视图是正三角形（如图3），则正四棱锥的体积是( )
A． |
B． |
C． |
D． |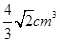
相关试题
,则
等于( )
在
处的切线平行于直线
,则
,其中
的单位是米，
的单位是秒，那么物体在
秒末的瞬时速度是（）
米/秒
米/秒
米/秒
米/秒
=（）相关知识点
推荐套卷
将一张边长为6 cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折叠并拼成一个有底的正四棱锥（底面是正方形，顶点在底面的射影为正方形的中心）模型，如图2放置，若正四棱锥的正视图是正三角形（如图3），则正四棱锥的体积是( )
| A． |
B． |
C． |
D． |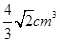
粤公网安备 44130202000953号