（本小题共13分）根据以往的成绩记录，甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
（1）求上图中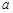
的值；
（2）甲队员进行一次射击，求命中环数大于7环的概率（频率当作概率使用）；
（3）由上图判断甲、乙两名队员中，哪一名队员的射击成绩更稳定（结论不需证明）
，求cos2x和
值．
，
若
，
，求
的值。
，
．求
和
的值．
，
，
，
，求
的值.
．
的值．
推荐套卷
（本小题共13分）根据以往的成绩记录，甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
（1）求上图中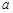的值；
（2）甲队员进行一次射击，求命中环数大于7环的概率（频率当作概率使用）；
（3）由上图判断甲、乙两名队员中，哪一名队员的射击成绩更稳定（结论不需证明）
粤公网安备 44130202000953号