已知R上的连续函数g(x)满足:①当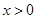 时,
时, 恒成立(
恒成立(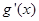 为函数
为函数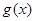 的导函数);②对任意的
的导函数);②对任意的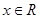 都有
都有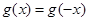 ,又函数
,又函数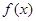 满足:对任意的
满足:对任意的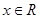 ,都有
,都有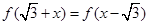 成立。当
成立。当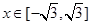 时,
时,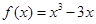 。若关于
。若关于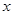 的不等式
的不等式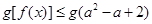 对
对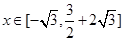 恒成立,则
恒成立,则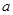 的取值范围是( )
的取值范围是( )
A.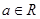 |
B.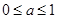 |
C.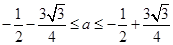 |
D.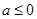 或 或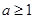 |
推荐套卷
已知R上的连续函数g(x)满足:①当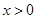 时,
时, 恒成立(
恒成立(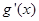 为函数
为函数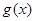 的导函数);②对任意的
的导函数);②对任意的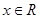 都有
都有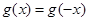 ,又函数
,又函数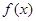 满足:对任意的
满足:对任意的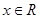 ,都有
,都有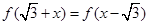 成立。当
成立。当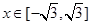 时,
时,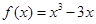 。若关于
。若关于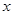 的不等式
的不等式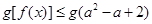 对
对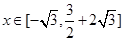 恒成立,则
恒成立,则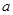 的取值范围是( )
的取值范围是( )
A.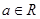 |
B.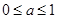 |
C.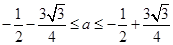 |
D.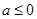 或 或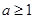 |