下列命题中，
①命题“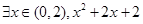
<
” 的否定是“
＞”；
②
是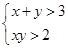
的充要条件；
③一个命题的逆命题为真，它的否命题也一定为真；
④“9＜
＜15”是“方程
表示椭圆”的充要条件．
⑤设
是以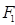
、
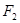为焦点的双曲线一点，且
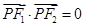，若
的面积为
，则双曲线的虚轴长为6；
其中真命题的是 （将正确命题的序号填上）
的定义域为___________．
的导数
，
，则
或
”时，假设命题的结论不成立的正确叙述是“ ”.
为纯虚数，
是虚数单位，则实数
的值是 ．相关知识点
推荐套卷
下列命题中，
①命题“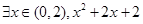<” 的否定是“＞”；
②是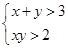的充要条件；
③一个命题的逆命题为真，它的否命题也一定为真；
④“9＜＜15”是“方程表示椭圆”的充要条件．
⑤设是以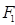、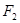为焦点的双曲线一点，且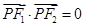，若的面积为，则双曲线的虚轴长为6；
其中真命题的是 （将正确命题的序号填上）
粤公网安备 44130202000953号