设某公司原有员工100人从事产品A的生产，平均每人每年创造产值t万元（t为正常数）．公司决定从原有员工中分流
（
）人去进行新开发的产品B的生产．分流后，继续从事产品A生产的员工平均每人每年创造产值在原有的基础上增长了
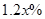．若要保证产品A的年产值不减少，则最多能分流的人数是（ ）
A． |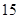
B． |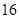
C． |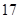
D． |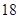
相关试题
满足当
时，都有
，且
是偶函数，则
与
的大小关系是
的图像有可能是（）
，则
（）
推荐套卷
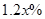设某公司原有员工100人从事产品A的生产，平均每人每年创造产值t万元（t为正常数）．公司决定从原有员工中分流（）人去进行新开发的产品B的生产．分流后，继续从事产品A生产的员工平均每人每年创造产值在原有的基础上增长了．若要保证产品A的年产值不减少，则最多能分流的人数是（ ）
| A． |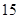
B． |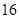
C． |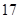
D． |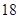
粤公网安备 44130202000953号