设函数f（x）＝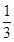
x3－ax（a＞0），g（x）＝bx2＋2b﹣1．
（1）若曲线y＝f（x）与y＝g（x）在它们的交点（1，c）处有相同的切线，求实数a，b的值；
（2）当b＝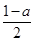
时，若函数h（x）＝f（x）＋g（x）在区间（﹣2，0）内恰有两个零点，求实数a的取值范围；
（3）当a＝1，b＝0时，求函数h（x）＝f（x）＋g（x）在区间[t，t＋3]上的最小值．
相关试题
。
，且
与
夹角为
。求：
；
的夹角。
,最小值为
,求a,b 的值.
和
中，
为数列
项和，
且
，
．
，求
.
（万元）与年产量
（吨）之间的函数关系式可以近似地表示为
，已知此生产线年产量最大为210吨。推荐套卷
设函数f（x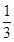）＝x3－ax（a＞0），g（x）＝bx2＋2b﹣1．
（1）若曲线y＝f（x）与y＝g（x）在它们的交点（1，c）处有相同的切线，求实数a，b的值；
（2）当b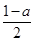＝时，若函数h（x）＝f（x）＋g（x）在区间（﹣2，0）内恰有两个零点，求实数a的取值范围；
（3）当a＝1，b＝0时，求函数h（x）＝f（x）＋g（x）在区间[t，t＋3]上的最小值．
粤公网安备 44130202000953号