设f '(x)和g'(x)分别是f(x)和g(x)的导函数，若f '(x)g'(x)≤0在区间I上恒成立，则称f(x)和g(x)在区间I上单调性相反．若函数f(x)＝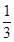
x3－2ax与g(x)＝x2＋2bx在开区间(a，b)上单调性相反(a＜b)，则b－a的最大值为______．
中，已知 
，则
的大小为
BD，平行则四边形ABCD一定是 .
中，
，则
=____ ___．
的解集为 ．推荐套卷
设f '(x)和g'(x)分别是f(x)和g(x)的导函数，若f '(x)g'(x)≤0在区间I上恒成立，则称f(x)和g(x)在区间I上单调性相反．若函数f(x)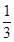＝x3－2ax与g(x)＝x2＋2bx在开区间(a，b)上单调性相反(a＜b)，则b－a的最大值为______．
粤公网安备 44130202000953号