二维空间中，圆的一维测度（周长）
，二维测度（面积）
；三维空间中，球的二维测度（表面积）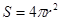
，三维测度（体积）
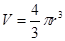.应用合情推理，若四维空间中，“超球”的三维测度
，则其四维测度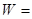
（ ）
A． |
B． |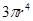
C． |
D． |
，函数
为奇函数，在点
处的切线方
，则
（ ）
的一部分图象如图所示，其中
，
，
，
中
，前
项的和为
，则
（ ）
，
，若
，则
（ ）
，
，则
（ ）
相关知识点
推荐套卷
二维空间中，圆的一维测度（周长），二维测度（面积）；三维空间中，球的二维测度（表面积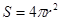），三维测度（体积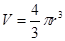）.应用合情推理，若四维空间中，“超球”的三维测度，则其四维测度（ ）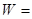
| A． |
B． |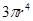
C． |
D． |
粤公网安备 44130202000953号