有如下四个结论:
①分别在两个平面内的两条直线一定是异面直线;
②过平面 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面 垂直;
垂直;
③ “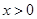 ”是“
”是“ ”的必要条件;
”的必要条件;
④命题“ ”的否定是“
”的否定是“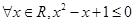 ”.
”.
其中正确结论的个数为( )
| A.4 | B.3 | C.2 | D.1 |
相关知识点
推荐套卷
有如下四个结论:
①分别在两个平面内的两条直线一定是异面直线;
②过平面 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面 垂直;
垂直;
③ “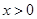 ”是“
”是“ ”的必要条件;
”的必要条件;
④命题“ ”的否定是“
”的否定是“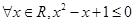 ”.
”.
其中正确结论的个数为( )
| A.4 | B.3 | C.2 | D.1 |