以下几个命题中:其中真命题的序号为 (写出所有真命题的序号)
①设A、B为两个定点,k为非零常数,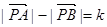 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③双曲线 有相同的焦点.
有相同的焦点.
④在平面内,到定点 的距离与到定直线
的距离与到定直线 的距离相等的点的轨迹是抛物线;
的距离相等的点的轨迹是抛物线;
相关知识点
推荐套卷
以下几个命题中:其中真命题的序号为 (写出所有真命题的序号)
①设A、B为两个定点,k为非零常数,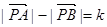 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O为坐标原点,若 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③双曲线 有相同的焦点.
有相同的焦点.
④在平面内,到定点 的距离与到定直线
的距离与到定直线 的距离相等的点的轨迹是抛物线;
的距离相等的点的轨迹是抛物线;