某学校准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175以下(不包括175cm)定义为“不合格”
(1)求甲队队员跳高成绩的中位数
(2)如果用分层抽样的方法从甲、乙两队所有的运动员中共抽取5人,则5人中“合格”与“不合格”的人数各为多少?
(3)从甲队178cm以上(包括178cm)选取2人,至少有一人在186cm以上(包括186cm)的概率为多少?
推荐套卷
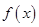
 ,
, .
. ,函数
,函数
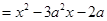 ,
,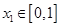 总存在
总存在 使
使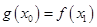 成立,求实数
成立,求实数 的取值范围.
的取值范围. 中,
中,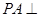 底面
底面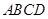 ,
,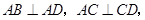
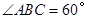 ,
,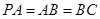 ,
, 是
是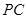 的中点.
的中点. 和平面
和平面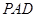 所成的角的大小;
所成的角的大小; 平面
平面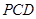 ;
;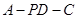 的正弦值.
的正弦值.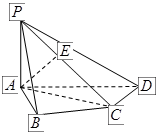
 :
: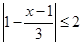 ,
,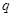 :
: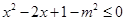 (
( ).若“非
).若“非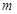 的取值范围.
的取值范围.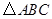 中,已知内角
中,已知内角 ,边
,边 .设内角
.设内角 ,周长为
,周长为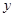 .
. 的解析式和定义域
的解析式和定义域  粤公网安备 44130202000953号
粤公网安备 44130202000953号