若存在实常数 和
和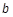 ,使得函数
,使得函数 和
和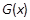 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: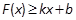 和
和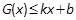 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和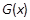 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是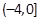 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
相关知识点
推荐套卷
若存在实常数 和
和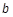 ,使得函数
,使得函数 和
和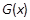 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: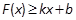 和
和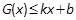 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和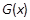 的“隔离直线”.已知函数
的“隔离直线”.已知函数 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是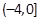 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |