一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示：
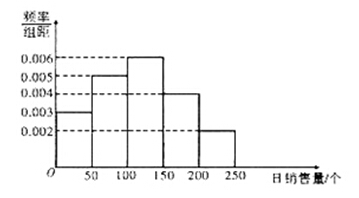
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
（1）求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率；
（2）用
表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望
及方差
.
相关试题
．
在
上的值域；
，不等式
恒成立，求
．
，
，
,
．
；
，求
的取值范围．
中，内角
的对边分别为
且
．
的值；
，求
．
且
．证明：
；
．
：
（
为参数），
：
（
为参数）．
对应的参数为
，
为
中点
到直线
（推荐套卷
一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示：
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
（1）求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率；
（2）用
表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望
及方差
.
粤公网安备 44130202000953号