某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：
 |
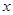2 |
3 |
4 |
5 |
6 |
 |
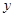2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
已知
，
，
(1)在下面坐标系中画出散点图；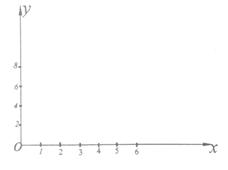
(2)计算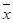
，
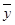，并求出线性回归方程；
(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?
中，
，
，你能用
，
表示向量
，
吗？
外的一点，过P作圆的切线，试求过两切点的切点弦所在的直线方程。
轴上，且过点A（1，4），B（2，
）的圆的方程。
中，A（-2，0 ），B（0，2）（
是变量），求相关知识点
推荐套卷
某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：
|
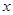2 |
3 |
4 |
5 |
6 |
|
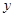2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
已知，，
(1)在下面坐标系中画出散点图；
(2)计算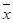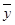，，并求出线性回归方程；
(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?
粤公网安备 44130202000953号