如图，斜面、水平轨道和半径R=2.5m的竖直半圆组成光滑轨道，水平轨道与半圆的最低点相切，轨道固定在水平面上。一个质量为m=0.1kg的小球从水平地面上A点斜向上抛出，并在半圆轨道最高点D水平进入轨道，然后沿斜面向上，达到最大高度h=6.25m。(不计空气阻力，小球在经过斜面与水平轨道连接处时不计能量损失。（g取10m/s2) 求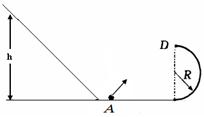
（1）小球抛出时的速度（角度可用三角函数表示）
（2）小球抛出点A到D的水平距离
（3）小球运动到半圆轨道最低点时球对轨道的压力
如图所示，电源电动势E=30V，内阻r=1Ω，电灯L上标有“25V， 25W”的字样，直流电动机M的线圈电阻R=2Ω．闭合电键，若电灯恰能正常发光，求：
（1）电路中的总电流I；
（2）电动机的热功率
；
（3）电动机输出的机械功率
。
如图所示，一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场，它刚好贴着下板右边缘飞出．已知匀强电场两极板长为L，间距为d，粒子的重力忽略不计。求：
（1）如果带电粒子的速度变为
v0，则离开电场时，沿场强方向偏转的距离为多少？
（2）如果带电粒子的速度变为v0，板长L不变，当它的竖直位移仍为d时，它的水平总位移为多少？
如图所示，质量为
=0.8
的小球A放在光滑的倾角
=30°绝缘斜面上，小球带正电，电荷量为
，在斜面上的B点固定一个电荷量为
的正点电荷，将小球A由距B点0.3处无初速度释放，求：（重力加速度
,静电力常量
） 
（1）A球刚释放时的加速度的大小
（2）当A球的动能最大时，A球与B点的距离。
一列简谐横波在x轴上传播，在t1=0和t2＝0.05s时，其波形图分别用如图所示的实线和虚线表示，求：
①这列波可能具有的波速。
②当波速为280m/s时，波的传播方向如何？以此波速传播时，x=8m处的质点P从平衡位置运动至波谷所需的最短时间是多少？
粤公网安备 44130202000953号