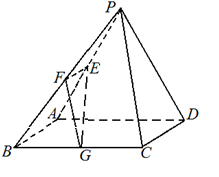
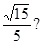已知在四棱锥 中,底面
中,底面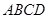 是边长为4的正方形,
是边长为4的正方形,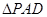 是正三角形,平面
是正三角形,平面 平面
平面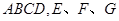 分别是
分别是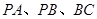 的中点.[Zx(1)求证:
的中点.[Zx(1)求证: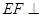 平面
平面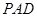 ;
;
(2)求平面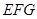 与平面
与平面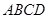 所成锐二面角的大小;
所成锐二面角的大小;
(3)若 为线段
为线段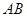 上靠近
上靠近 的一个动点,问当
的一个动点,问当 长度等于多少时,直线
长度等于多少时,直线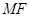 与平面
与平面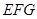 所成角的正弦值等于
所成角的正弦值等于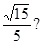
推荐套卷
已知在四棱锥 中,底面
中,底面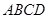 是边长为4的正方形,
是边长为4的正方形,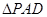 是正三角形,平面
是正三角形,平面 平面
平面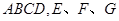 分别是
分别是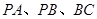 的中点.[Zx(1)求证:
的中点.[Zx(1)求证: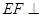 平面
平面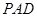 ;
;
(2)求平面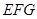 与平面
与平面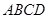 所成锐二面角的大小;
所成锐二面角的大小;
(3)若 为线段
为线段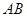 上靠近
上靠近 的一个动点,问当
的一个动点,问当 长度等于多少时,直线
长度等于多少时,直线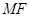 与平面
与平面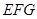 所成角的正弦值等于
所成角的正弦值等于