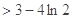已知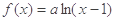 ,
,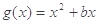 ,
,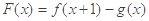 ,其中
,其中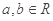 。
。
(1)若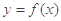 与
与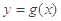 的图像在交点(2,
的图像在交点(2,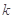 )处的切线互相垂直,
)处的切线互相垂直,
求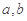 的值;
的值;
(2)若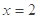 是函数
是函数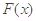 的一个极值点,
的一个极值点,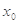 和1是
和1是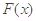 的两个零点,
的两个零点,
且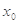 ∈(
∈(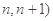
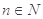 ,求
,求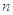 ;
;
(3)当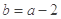 时,若
时,若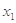 ,
, 是
是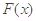 的两个极值点,当|
的两个极值点,当|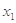 -
- |>1时,
|>1时,
求证:|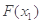 -
-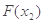 |
|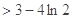
推荐套卷
已知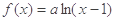 ,
,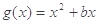 ,
,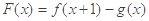 ,其中
,其中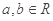 。
。
(1)若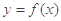 与
与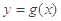 的图像在交点(2,
的图像在交点(2,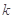 )处的切线互相垂直,
)处的切线互相垂直,
求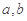 的值;
的值;
(2)若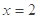 是函数
是函数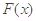 的一个极值点,
的一个极值点,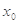 和1是
和1是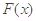 的两个零点,
的两个零点,
且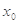 ∈(
∈(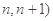
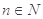 ,求
,求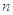 ;
;
(3)当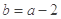 时,若
时,若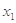 ,
, 是
是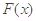 的两个极值点,当|
的两个极值点,当|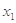 -
- |>1时,
|>1时,
求证:|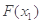 -
-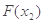 |
|