设双曲线
-
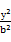=1(a>0,b>0)的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若
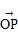=λ
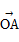+μ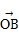
(λ,μ∈R),λμ=
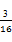,则该双曲线的离心率为( )
A． |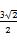
B． |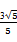
C． |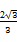
D． |
相关试题
，且S100＝145，则a2＋a4＋…＋a100的值为（）
相关知识点
推荐套卷
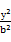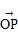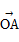设双曲线-=1(a>0,b>0)的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若=λ+μ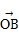(λ,μ∈R),λμ=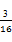,则该双曲线的离心率为( )
| A． |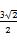
B． |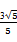
C． |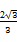
D． |
粤公网安备 44130202000953号