在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，设O为坐标原点，点P的坐标为
记
.
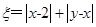（1）求随机变量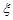
的最大值，并求事件“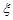取得最大值”的概率；
（2）求随机变量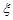的分布列和数学期望.
相关试题
的值。
中，内角
所对边
，
，
，且向量
共线，
（2）若边
，求
中，已知
，
=（3，－4），
；
；
的坐标.
中，
且
成等比数列，求数列
．推荐套卷
在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，设O为坐标原点，点P的坐标为记.
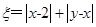（1）求随机变量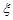 的最大值，并求事件“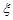取得最大值”的概率；
（2）求随机变量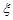的分布列和数学期望.
粤公网安备 44130202000953号