某班有60名学生，其中正、副班长各1人，现要选派5人参加一项社区活动，要求正、副班长至少1人参加，问共有多少种选派方法？下面是学生提供的四个计算式，其中错误的是（ ）
A． |
B． |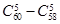
C． |
D． |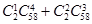
是函数
的零点，若
，则
的值满足
的图象与直线
相切, 则
上的偶函数
满足：对任意的
，有
.则
，则函数
的图像大致是 
，则
的值是
推荐套卷
某班有60名学生，其中正、副班长各1人，现要选派5人参加一项社区活动，要求正、副班长至少1人参加，问共有多少种选派方法？下面是学生提供的四个计算式，其中错误的是（ ）
| A． |
B． |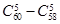
C． |
D． |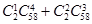
粤公网安备 44130202000953号