设e1、e2是平面内一组基向量，且a＝e1＋2e2，b＝－e1＋e2，则向量e1＋e2可以表示为另一组基向量a、b的线性组合，即e1＋e2＝ma＋nb，则m、n分别为（ ）
A． |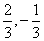
B． |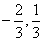
C． |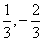
D． |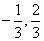
成等比数列，
分别成等差数列，且
，则
的值等于（）
，且
，则（）
的图象可能是（）
等于（ ）
推荐套卷
设e1、e2是平面内一组基向量，且a＝e1＋2e2，b＝－e1＋e2，则向量e1＋e2可以表示为另一组基向量a、b的线性组合，即e1＋e2＝ma＋nb，则m、n分别为（ ）
| A． |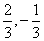
| B． |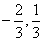
| C． |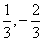
| D． |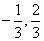
粤公网安备 44130202000953号