设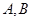 分别为椭圆
分别为椭圆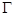 :
: 的左右顶点,
的左右顶点,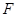 为右焦点,
为右焦点, 为
为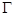 在点
在点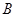 处的切线,
处的切线,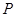 为
为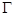 上异于
上异于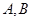 的一点,直线
的一点,直线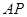 交
交 于
于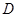 ,
,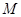 为
为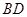 中点,有如下结论:①
中点,有如下结论:①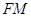 平分
平分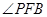 ;②
;② 与椭圆
与椭圆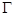 相切;③
相切;③ 平分
平分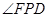 ;④使得
;④使得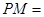
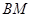 的点
的点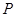 不存在.其中正确结论的序号是_____________.
不存在.其中正确结论的序号是_____________.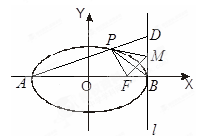
推荐套卷
设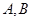 分别为椭圆
分别为椭圆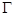 :
: 的左右顶点,
的左右顶点,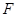 为右焦点,
为右焦点, 为
为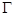 在点
在点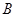 处的切线,
处的切线,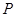 为
为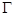 上异于
上异于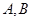 的一点,直线
的一点,直线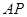 交
交 于
于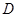 ,
,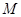 为
为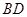 中点,有如下结论:①
中点,有如下结论:①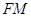 平分
平分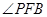 ;②
;② 与椭圆
与椭圆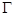 相切;③
相切;③ 平分
平分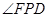 ;④使得
;④使得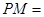
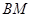 的点
的点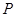 不存在.其中正确结论的序号是_____________.
不存在.其中正确结论的序号是_____________.