设函数f（x）的定义域为D,若存在非零实数l使得对于任意x∈M（M⊆D）有x+l∈D，且f（x＋l）≥f(x)，则称f(x)为M上的l高调函数，如果定义域为R的函数f(x)是奇函数，当x≥0时，f（x）＝｜x－a2｜－a2，且f(x)为R上的8高调函数，那么实数a的取值范围是( )
A.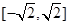 
B. 
C. 
D. 
相关试题
且
，则下列不等式中一定成立的是（）
的公差为
,若
成等比数列, 则
（）
，则下列不等关系正确的是（）
的通项公式
则它的公差为（）
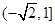
推荐套卷
设函数f（x）的定义域为D,若存在非零实数l使得对于任意x∈M（M⊆D）有x+l∈D，且f（x＋l）≥f(x)，则称f(x)为M上的l高调函数，如果定义域为R的函数f(x)是奇函数，当x≥0时，f（x）＝｜x－a2｜－a2，且f(x)为R上的8高调函数，那么实数a的取值范围是( )
A. 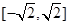B. C. D.
粤公网安备 44130202000953号