设f(x)=asinx+bcos2x,其中a,b∈R,ab≠0.若f(x)≤
对一切x∈R恒成立,则
①f
=0;
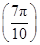②︱f
︱<︱f
︱;
③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是[kπ+
,kπ+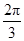
](k∈Z);
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交.
以上结论正确的是 (写出所有正确结论的编号).
相关知识点
推荐套卷
设f(x)=asinx+bcos2x,其中a,b∈R,ab≠0.若f(x)≤对一切x∈R恒成立,则
①f=0;
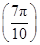②︱f︱<︱f︱;
③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是[kπ+,kπ+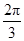](k∈Z);
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交.
以上结论正确的是 (写出所有正确结论的编号).
粤公网安备 44130202000953号