)在计算“1×2+2×3+…+n(n+1)”时,某同学学到了如下一种方法:先改写第k项:
k(k+1)=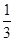 [k(k+1)(k+2)-(k-1)k(k+1)],
[k(k+1)(k+2)-(k-1)k(k+1)],
由此得1×2=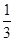 (1×2×3-0×1×2),
(1×2×3-0×1×2),
2×3=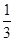 (2×3×4-1×2×3),…,
(2×3×4-1×2×3),…,
n(n+1)=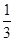 [n(n+1)(n+2)-(n-1)n(n+1)].
[n(n+1)(n+2)-(n-1)n(n+1)].
相加,得1×2+2×3+…+n(n+1)=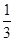 n(n+1)(n+2).
n(n+1)(n+2).
类比上述方法,请你计算“1×2×3+2×3×4+…+n(n+1)(n+2)”,其结果为 .
相关知识点
推荐套卷
 的方程为
的方程为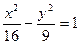 ,则其离心
,则其离心 =________
=________ ___
___ ______________
______________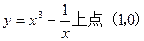 处的切线方程
处的切线方程 是____________
是____________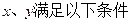
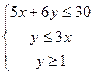 则
则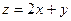 的最小值是___________
的最小值是___________ ,那么它的焦距为____________
,那么它的焦距为____________ 粤公网安备 44130202000953号
粤公网安备 44130202000953号