设e1，e2，e3，e4是某平面内的四个单位向量，其中e1⊥e2，e3与e4的夹角为45°，对这个平面内的任意一个向量a＝xe1＋ye2，规定经过一次“斜二测变换”得到向量a1＝xe3＋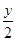
e4.设向量t1＝－3e3－2e4是经过一次“斜二测变换”得到的向量，则|t|是( )
| A．5 | B． |
C．73 | D． |
，下面不等式成立的是（ ）
等于（ ）
的最大值是（ ）
= （ ）
有相同定义域的是（ ）
推荐套卷
设e1，e2，e3，e4是某平面内的四个单位向量，其中e1⊥e2，e3与e4的夹角为45°，对这个平面内的任意一个向量a＝xe1＋ye2，规定经过一次“斜二测变换”得到向量a1＝xe3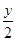＋e4.设向量t1＝－3e3－2e4是经过一次“斜二测变换”得到的向量，则|t|是( )
| A．5 | B． |
C．73 | D． |
粤公网安备 44130202000953号