如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0( ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )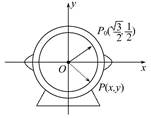
A.y=sin(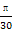 t+ t+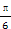 ) ) |
B.y=sin(-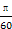 t- t-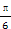 ) ) |
C.y=sin(-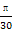 t+ t+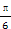 ) ) |
D.y=sin(-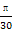 t- t- ) ) |
相关知识点
推荐套卷
如图,为了研究钟表与三角函数的关系,建立了如图所示的坐标系,设秒针针尖位置P(x,y).若初始位置为P0( ,
, ),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为( )
A.y=sin(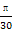 t+ t+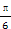 ) ) |
B.y=sin(-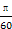 t- t-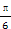 ) ) |
C.y=sin(-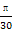 t+ t+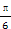 ) ) |
D.y=sin(-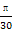 t- t- ) ) |