(13分)已知圆O：x2＋y2＝3的半径等于椭圆E：
＝1(a>b>0)的短半轴长，椭圆E的右焦点F在圆O内，且到直线l：y＝x－
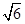的距离为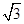
－
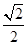，点M是直线l与圆O的公共点，设直线l交椭圆E于不同的两点A(x1，y1)，B(x2，y2)．
(1)求椭圆E的方程；
(2)求证：|AF|－|BF|＝|BM|－|AM|.
相关试题
的前
项和为
,
. 
,求数列
的前
项和
.
，
.
；
与
、
均相切，切点分别为（
）、（
），且
，求证：
.
.
的单调区间；
与
有三个不同的交点，求实数
的取值范围.
.
的最小正周期；
在
处取得最大值，求
的值;
的单调递增区间.
为等差数列，且
.
项和
；
满足
求数列推荐套卷
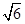(13分)已知圆O：x2＋y2＝3的半径等于椭圆E：＝1(a>b>0)的短半轴长，椭圆E的右焦点F在圆O内，且到直线l：y＝x－的距离为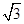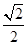－，点M是直线l与圆O的公共点，设直线l交椭圆E于不同的两点A(x1，y1)，B(x2，y2)．
(1)求椭圆E的方程；
(2)求证：|AF|－|BF|＝|BM|－|AM|.
粤公网安备 44130202000953号