已知直线l：y＝x＋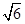
，圆O：x2＋y2＝5，椭圆E：
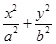＝1(a>b>0)的离心率e＝
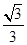，直线l被圆O截得的弦长与椭圆的短轴长相等．
(1)求椭圆E的方程；
(2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两条切线的斜率之积为定值．
相关试题
．
≤
．推荐套卷
已知直线l：y＝x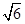＋，圆O：x2＋y2＝5，椭圆E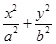：＝1(a>b>0)的离心率e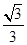＝，直线l被圆O截得的弦长与椭圆的短轴长相等．
(1)求椭圆E的方程；
(2)过圆O上任意一点P作椭圆E的两条切线，若切线都存在斜率，求证：两条切线的斜率之积为定值．
粤公网安备 44130202000953号