给出以下四个命题,所有真命题的序号为________.
①从总体中抽取样本(x1,y1),(x2,y2),…,(xn,yn),若记 ,
, ,则回归直线y=bx+a必过点(
,则回归直线y=bx+a必过点( ,
,  ).
).
②将函数y=cos 2x的图象向右平移 个单位,得到函数y=sin
个单位,得到函数y=sin 的图象;
的图象;
③已知数列{an},那么“对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件.
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”.
相关知识点
推荐套卷
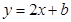 与曲线
与曲线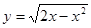 有且仅有一个公共点,则
有且仅有一个公共点,则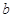 的范围是
的范围是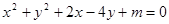 与直线
与直线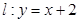 相切,且圆D与圆C关
相切,且圆D与圆C关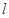 对称,则圆D的方程是___________。
对称,则圆D的方程是___________。 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为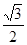 ,则
,则 的值是___________。
的值是___________。 绕着它与
绕着它与 轴的交点顺时针旋转
轴的交点顺时针旋转 所得的直线方程为___________。
所得的直线方程为___________。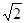 的四棱锥
的四棱锥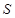 -
- 的底面是边长为1的正方形,点
的底面是边长为1的正方形,点 、
、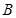 、
、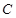 、
、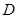 均在半径为1的同一球面上,则底面
均在半径为1的同一球面上,则底面 粤公网安备 44130202000953号
粤公网安备 44130202000953号