若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤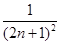 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<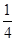 .
.
推荐套卷
若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤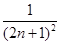 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|<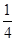 .
.