如图,储油灌的表面积 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.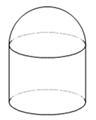
⑴试用半径 表示出储油灌的容积
表示出储油灌的容积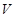 ,并写出
,并写出 的范围.
的范围.
⑵当圆柱高 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积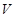 最大?
最大?
相关知识点
推荐套卷
如图,储油灌的表面积 为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
为定值,它的上部是半球,下部是圆柱,半球的半径等于圆柱底面半径.
⑴试用半径 表示出储油灌的容积
表示出储油灌的容积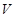 ,并写出
,并写出 的范围.
的范围.
⑵当圆柱高 与半径
与半径 的比为多少时,储油灌的容积
的比为多少时,储油灌的容积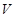 最大?
最大?