抛物线有光学性质：由其焦点射出的光线经抛物线折射后，沿平行于抛物线对称轴的方向射出。现已知抛物线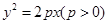
的焦点为F，过抛物线上点
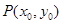的切线为
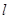，过P点作平行于x轴的直线m，过焦点F作平行于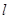的直线交m于M，则
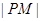的长为（ ）
A． |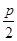
B． |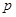
C． |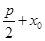
D． |
，则
的值为（）
等于（）
，且
是第二象限角，则
的值等于（）
的定义域为（）
，
，则
等于（）
相关知识点
推荐套卷
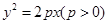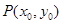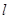抛物线有光学性质：由其焦点射出的光线经抛物线折射后，沿平行于抛物线对称轴的方向射出。现已知抛物线的焦点为F，过抛物线上点的切线为，过P点作平行于x轴的直线m，过焦点F作平行于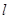的直线交m于M，则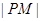的长为（ ）
| A． |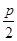
B． |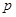
C． |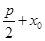
D． |
粤公网安备 44130202000953号