已知椭圆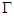 :
: .
.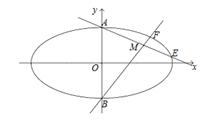
(1)椭圆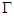 的短轴端点分别为
的短轴端点分别为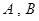 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆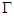 交于
交于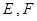 两点,其中点
两点,其中点 满足
满足 ,且
,且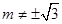 .
.
①证明直线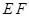 与
与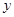 轴交点的位置与
轴交点的位置与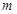 无关;
无关;
②若∆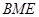 面积是∆
面积是∆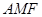 面积的5倍,求
面积的5倍,求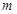 的值;
的值;
(2)若圆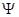 :
: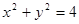 .
. 是过点
是过点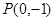 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中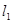 交圆
交圆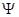 于
于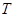 、
、 两点,
两点,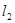 交椭圆
交椭圆 于另一点
于另一点 .求
.求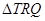 面积取最大值时直线
面积取最大值时直线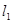 的方程.
的方程.
推荐套卷
已知椭圆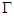 :
: .
.
(1)椭圆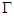 的短轴端点分别为
的短轴端点分别为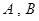 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆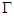 交于
交于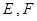 两点,其中点
两点,其中点 满足
满足 ,且
,且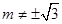 .
.
①证明直线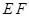 与
与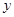 轴交点的位置与
轴交点的位置与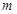 无关;
无关;
②若∆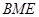 面积是∆
面积是∆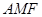 面积的5倍,求
面积的5倍,求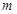 的值;
的值;
(2)若圆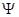 :
: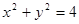 .
. 是过点
是过点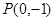 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中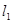 交圆
交圆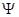 于
于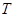 、
、 两点,
两点,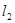 交椭圆
交椭圆 于另一点
于另一点 .求
.求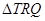 面积取最大值时直线
面积取最大值时直线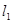 的方程.
的方程.