某人定制了一批地砖,每块地砖(如图1所示)是边长为40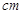 的正方形
的正方形 ,点
,点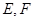 分别在边
分别在边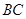 和
和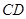 上,△
上,△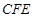 ,△
,△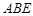 和四边形
和四边形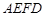 均由单一材料制成,制成△
均由单一材料制成,制成△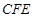 ,△
,△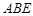 和四边形
和四边形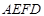 的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形
的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形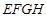 .则当
.则当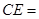
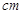 时,定制这批地砖所需的材料费用最省?
时,定制这批地砖所需的材料费用最省?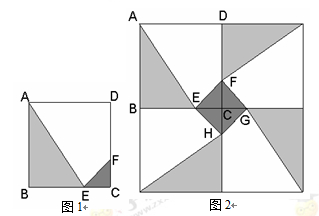
推荐套卷
某人定制了一批地砖,每块地砖(如图1所示)是边长为40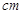 的正方形
的正方形 ,点
,点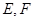 分别在边
分别在边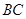 和
和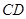 上,△
上,△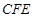 ,△
,△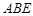 和四边形
和四边形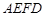 均由单一材料制成,制成△
均由单一材料制成,制成△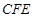 ,△
,△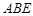 和四边形
和四边形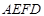 的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形
的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形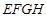 .则当
.则当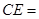
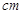 时,定制这批地砖所需的材料费用最省?
时,定制这批地砖所需的材料费用最省?