(1)如图,ABC在平面外,AB∩=P,BC∩=Q,AC∩=R,求证:P,Q,R三点共线.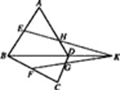
(2)如图,空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点, 且EH与FG相交于点K. 求证:EH,BD,FG三条直线相交于同一点.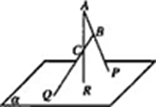
相关试题
，
，且
．
；
．
=（−cosx,sinx），
=（cosx ,
），函数f(x)=
,
夹角的大小．
,定义
.
的单调递减区间；
的取值集合.
的最小正周期；
，不等式f(x)＞m－3恒成立，求实数m的取值范围.
=（cos
,sin
=(cos
且
的夹角为
,三角形的面积S=
,求a+b（a、b、c分别∠A、∠B、∠C所对的边）推荐套卷
(1)如图,ABC在平面外,AB∩=P,BC∩=Q,AC∩=R,求证:P,Q,R三点共线.
(2)如图,空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点, 且EH与FG相交于点K. 求证:EH,BD,FG三条直线相交于同一点.
粤公网安备 44130202000953号