如图所示, 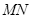 和
和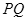 为固定在绝缘水平面上两平行光滑金属导轨,导轨左端
为固定在绝缘水平面上两平行光滑金属导轨,导轨左端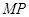 间接有阻值为
间接有阻值为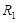 =
=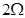 导线;导轨右端接有与水平轨道相切、半径
导线;导轨右端接有与水平轨道相切、半径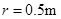 内壁光滑的半圆金属轨道。导轨间距
内壁光滑的半圆金属轨道。导轨间距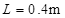 ,电阻不计。导轨所在平面
,电阻不计。导轨所在平面 区域内有竖直向上
区域内有竖直向上 的匀强磁场。导轨上长度也为
的匀强磁场。导轨上长度也为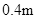 、质量
、质量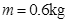 、电阻
、电阻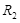 =
=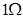 的金属棒
的金属棒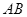 以
以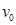 =
=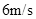 速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度
速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触。已知重力加速度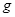 =
=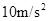 。求:
。求: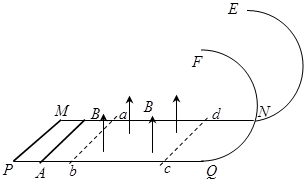
(1)金属棒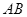 刚滑出磁场右边界
刚滑出磁场右边界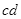 时的速度
时的速度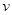 的大小;
的大小;
(2)金属棒滑过磁场区的过程中,导线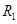 中产生的热量
中产生的热量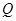 。
。

 ,R1=3.0
,R1=3.0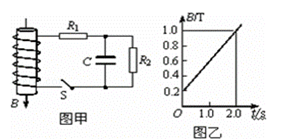

 的物体在于水平方向成
的物体在于水平方向成 的拉力F作用下,由静止开始运动,运动
的拉力F作用下,由静止开始运动,运动 后立即撤去拉力F,物体在水平面继续运动
后立即撤去拉力F,物体在水平面继续运动 后速度减为零,物体在整个过程中运动
后速度减为零,物体在整个过程中运动 ,求拉力F的大小(已知:
,求拉力F的大小(已知: ,
, ,
, )。
)。
 的小物块以
的小物块以 的初速度沿无限长的粗糙斜面向上滑,
的初速度沿无限长的粗糙斜面向上滑, 后物块到达最高点,已知斜面的倾角
后物块到达最高点,已知斜面的倾角 ,
, ,求物体与斜面间的动摩擦因数
,求物体与斜面间的动摩擦因数
 )。
)。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号