如图所示，空间存在水平向右的匀强电场. 在竖直平面内 建立平面直角坐标系，在坐标系的一象限内固定绝缘光滑的半径为R的1/4圆周轨道AB，轨道的两端在坐标轴上。质量为m的带正电的小球从轨道的A端由静止开始滚下，已知重力为电场力的2倍，求：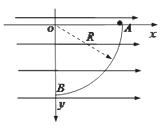
（1）小球在轨道最低点B时对轨道的压力；
（2）小球脱离B点后开始计时，经过多长时间小球运动到B点的正下方？并求出此时小球距B的竖直高度h是多大？
如图所示，在xOy平面的第一象限内有平行于y轴的有界匀强电场，方向如图，一个电子以垂直于y轴的初速度v0从P点射入电场中，P点的坐标为（0，y0）．当匀强电场的场强为E1时电子从A点射出，A点坐标为（xA，0），当场强为E2时，电子从B点射出，B点坐标为（xB，0），设电子的电荷量为e，质量为m，不计重力，其中xA、xB为已知量，其余量未知．
（1）求匀强电场的场强E1与E2的比值．
（2）若在第四象限过Q点放一张垂直于xOy平面的感光胶片，位置如图所示，Q点的坐标为（0，－y0），求感光胶片上曝光点的横坐标x′A和x′B的比值．
如图，真空中xOy平面直角坐标系上的A、B、C三点构成等边三角形，边长L＝2.0 m．若将电荷量均为q＝＋2.0×10－6 C的两点电荷分别固定在A、B点，已知静电力常量k＝9×109 N·m2/C2，求：
（1）两点电荷间的库仑力大小；
（2）C点的电场强度的大小和方向．
(12分)虚线MN下方有竖直向上的匀强电场，场强大小E=2×103V/m，MN上方有一竖直长为L=0.5m的轻质绝缘杆，杆的上下两端分别固定一带电小球A、B(可看成质点)，质量均为m=0.01kg，A带电量为
；B带电量
，B到MN的距离h=0.05m。现将杆由静止释放（g取10m/s2），求：
（1）小球B在匀强电场中，而A还未进入电场时，两小球的加速度大小。
（2）从开始运动到A刚要进入匀强电场过程的时间。
(12分)ABC表示竖直放在电场强度为E=104V/m的水平匀强电场中的绝缘光滑轨道，其中轨道的BC部分是半径为R的1/4圆环，轨道的水平部分与半圆环相切。A为水平轨道上的一点，而且AB=R=0.2m，把一质量m=0.1kg，带电量为
的小球，放在A点由静止释放后，求：（g=10m/s2）
（1）小球到达C点的速度大小
（2）小球在C点时，轨道受到的压力大小
、电量为
的带电微粒以2m/s的速度从水平放置的平行金属板A、B正中央水平飞入板间，已知板长L=10cm，板间距离d=2cm
粤公网安备 44130202000953号