设函数y=f(x)在(-∞,+∞)内有定义，对于给定的正数k，定义函数：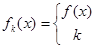
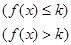,取函数f(x)=2-x-e-x，若对任意的x∈(-∞,+ ∞)，恒有fk(x)＝f(x)，则( )
| A．k的最大值为2 | B．k的最小值为2 |
| C．k的最大值为1 | D．k的最小值为1 |
相关试题
推荐套卷
设函数y=f(x)在(-∞,+∞)内有定义，对于给定的正数k，定义函数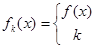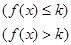： ,取函数f(x)=2-x-e-x，若对任意的x∈(-∞,+ ∞)，恒有fk(x)＝f(x)，则( )
| A．k的最大值为2 | B．k的最小值为2 |
| C．k的最大值为1 | D．k的最小值为1 |
粤公网安备 44130202000953号