定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)成为平面斜坐标系. 在平面斜坐标系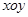 中,
中,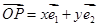 (其中
(其中 ,
,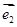 分别是斜坐标系
分别是斜坐标系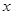 轴,
轴,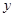 轴正方向上的单位向量,
轴正方向上的单位向量,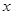 ,
, ,
,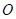 为坐标系原点),则有序数对
为坐标系原点),则有序数对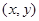 称为点
称为点 的斜坐标,在平面斜坐标系
的斜坐标,在平面斜坐标系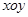 中,
中,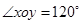 ,点
,点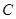 的斜坐标为
的斜坐标为 ,则以点
,则以点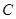 位圆心,2为半径的圆在斜坐标系
位圆心,2为半径的圆在斜坐标系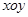 中的方程为( )
中的方程为( )
A. |
B. |
C. |
D.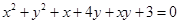 |
推荐套卷
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)成为平面斜坐标系. 在平面斜坐标系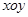 中,
中,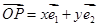 (其中
(其中 ,
,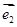 分别是斜坐标系
分别是斜坐标系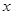 轴,
轴,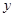 轴正方向上的单位向量,
轴正方向上的单位向量,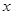 ,
, ,
,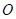 为坐标系原点),则有序数对
为坐标系原点),则有序数对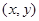 称为点
称为点 的斜坐标,在平面斜坐标系
的斜坐标,在平面斜坐标系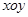 中,
中,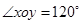 ,点
,点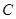 的斜坐标为
的斜坐标为 ,则以点
,则以点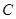 位圆心,2为半径的圆在斜坐标系
位圆心,2为半径的圆在斜坐标系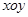 中的方程为( )
中的方程为( )
A. |
B. |
C. |
D.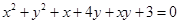 |