已知边长分别为a、b、c的三角形ABC面积为S，内切圆O半径为r，连接OA、OB、OC，则三角形OAB、OBC、OAC的面积分别为
cr、ar、br，由S=cr+ar+br得r=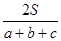
，类比得若四面体的体积为V,四个面的面积分别为A、B、C、D，则内切球的半径R=_____________.
的前
项和为
，
，则
．
，
，若
，则
．
的焦点为圆心，以焦点到准线的距离为半径的圆被双曲线
的
推荐套卷
已知边长分别为a、b、c的三角形ABC面积为S，内切圆O半径为r，连接OA、OB、OC，则三角形OAB、OBC、OAC的面积分别为cr、ar、br，由S=cr+ar+br得r=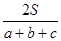，类比得若四面体的体积为V,四个面的面积分别为A、B、C、D，则内切球的半径R=_____________.
粤公网安备 44130202000953号