设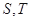 是
是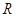 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从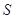 到
到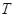 的函数
的函数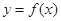 满足;
满足;
(i)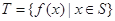 ;(ii)对任意
;(ii)对任意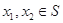 ,当
,当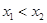 时,恒有
时,恒有 .
.
那么称这两个集合“保序同构”.现给出以下3对集合:
①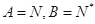 ;
;
②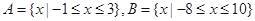 ;
;
③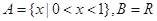 .
.
其中,“保序同构”的集合对的序号是____________(写出所有“保序同构”的集合对的序号)
推荐套卷
设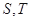 是
是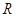 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从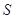 到
到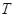 的函数
的函数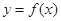 满足;
满足;
(i)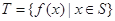 ;(ii)对任意
;(ii)对任意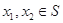 ,当
,当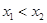 时,恒有
时,恒有 .
.
那么称这两个集合“保序同构”.现给出以下3对集合:
①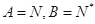 ;
;
②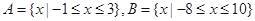 ;
;
③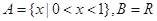 .
.
其中,“保序同构”的集合对的序号是____________(写出所有“保序同构”的集合对的序号)