某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
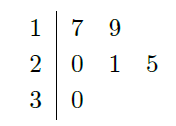
(Ⅰ) 根据茎叶图计算样本均值；
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人；
(Ⅲ) 从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
是
的导函数。
的最大值和最小正周期；
的值。
（其中A>0，
）的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个最低点为
.
的解析式；
，求
求值：
（Ⅰ）
；
.
，求
的值。
，
，求
以及
的值．推荐套卷
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
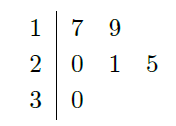
(Ⅰ) 根据茎叶图计算样本均值；
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人；
(Ⅲ) 从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
粤公网安备 44130202000953号