已知椭圆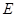
的中心在坐标原点，焦点在
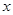轴上，离心率为
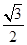，且过双曲线
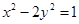的顶点．
（1）求椭圆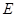的标准方程；
（2）命题：“设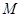
、
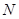是双曲线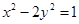上关于它的中心对称的任意两点，
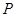为该双曲线上的动点，若直线
、
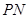均存在斜率，则它们的斜率之积为定值”．试类比上述命题，写出一个关于椭圆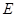的类似的正确命题，并加以证明和求出此定值；
（3）试推广（Ⅱ）中的命题，写出关于方程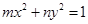
（
，
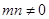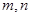不同时为负数）的曲线的统一的一般性命题（不必证明）.
相关试题
（
）
满足什么条件时，z是实数？
（2）
（4）
中，
⊥面
，
，
，
为
的中点.
；
的余弦值；
，使得
？请证明你的结论.
，求导函数
，并确定
的单调区间．
，
∈R
时,
取得极值，求
内为增函数，求推荐套卷
已知椭圆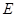的中心在坐标原点，焦点在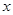轴上，离心率为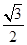，且过双曲线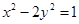的顶点．
（1）求椭圆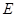的标准方程；
（2）命题：“设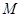、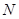是双曲线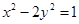上关于它的中心对称的任意两点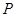， 为该双曲线上的动点，若直线、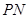均存在斜率，则它们的斜率之积为定值”．试类比上述命题，写出一个关于椭圆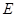的类似的正确命题，并加以证明和求出此定值；
（3）试推广（Ⅱ）中的命题，写出关于方程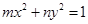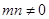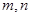（，不同时为负数）的曲线的统一的一般性命题（不必证明）.
粤公网安备 44130202000953号