已知圆 ,椭圆
,椭圆 .
.
(Ⅰ)若点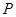 在圆
在圆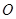 上,线段
上,线段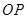 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点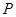 的横坐标;
的横坐标;
(Ⅱ)现有如下真命题:
“过圆 上任意一点
上任意一点 作椭圆
作椭圆 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;
“过圆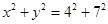 上任意一点
上任意一点 作椭圆
作椭圆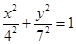 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”.
据此,写出一般结论,并加以证明.
推荐套卷
已知圆 ,椭圆
,椭圆 .
.
(Ⅰ)若点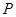 在圆
在圆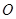 上,线段
上,线段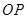 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点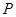 的横坐标;
的横坐标;
(Ⅱ)现有如下真命题:
“过圆 上任意一点
上任意一点 作椭圆
作椭圆 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;
“过圆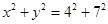 上任意一点
上任意一点 作椭圆
作椭圆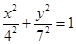 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”.
据此,写出一般结论,并加以证明.