挪威数学家阿贝尔，曾经根据阶梯形图形的两种不同分割(如下图)，利用它们的面积关系发现了一个重要的恒等式一阿贝尔公式：
a1b1+a2b2+a3b3+ +anbn=a1(b1-b2)+L2(b2-b3)+L3(b3-b4)+ +Ln-1(bn-1-bn)+Lnbn
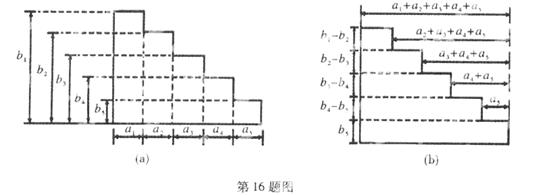
则其中：(I)L3= ；(Ⅱ)Ln= ．
|=6，|
|=6，|
|=
，则边BC的长是.
在[1,2]上的最大值为。
的二项展开式中系数最大的项.推荐套卷
挪威数学家阿贝尔，曾经根据阶梯形图形的两种不同分割(如下图)，利用它们的面积关系发现了一个重要的恒等式一阿贝尔公式：
a1b1+a2b2+a3b3+ +anbn=a1(b1-b2)+L2(b2-b3)+L3(b3-b4)+ +Ln-1(bn-1-bn)+Lnbn
则其中：(I)L3= ；(Ⅱ)Ln= ．
粤公网安备 44130202000953号